[F-Lab 모각코 챌린지 19일차] HashMap put() 뜯어보기 / 자료구조 트리 개념
TIL
- HashMap put() 뜯어보기
- 자료구조 트리 개념
HashMap put() 뜯어보기
public static void main(String[] args) {
HashMap<String, String> map = new HashMap<>();
map.put("1", "짱구");
map.put("2", "철수");
map.put("1", "맹구");
}public V put(K key, V value) {
// hash()는 보조 해시 함수로 해시충돌을 최대한 방지함
return putVal(hash(key), key, value, false, true);
}static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}주어진 key의 해시코드를 계산한 후(key.hashCode()), XOR 연산을 통해 해시의 상위 비트를 하위 비트로 퍼뜨린다. 이를 통해 일부 해시충돌을 방지하고 최대한 낮은 비트까지 활용할 수 있다. (주석 읽어봤으나 이 정도까지만 이해 가능🤣)
ℹ HashMap의 hash() 주석
Computes key.hashCode() and spreads (XORs) higher bits of hash to lower. Because the table uses power-of-two masking, sets of hashes that vary only in bits above the current mask will always collide. (Among known examples are sets of Float keys holding consecutive whole numbers in small tables.) So we apply a transform that spreads the impact of higher bits downward. There is a tradeoff between speed, utility, and quality of bit-spreading. Because many common sets of hashes are already reasonably distributed (so don't benefit from spreading), and because we use trees to handle large sets of collisions in bins, we just XOR some shifted bits in the cheapest possible way to reduce systematic lossage, as well as to incorporate impact of the highest bits that would otherwise never be used in index calculations because of table bounds.
/**
* hash: key에 대한 해시값
* key : 저장하려는 키
* value : 저장하려는 값
* onlyIfAbsent : true인 경우, 기존 값을 변경하지 않는다.
* evict : false인 경우, table이 생성 상태에 있다.
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node<K,V>[] tab; // 해시버킷
Node<K,V> p; // 기존에 저장 된 Node
int n, i; // n: 해시버킷 사이즈, i: 해시버킷 인덱스
// 해당 HashMap 객체에 데이터를 처음 저장할 때, 동작한다.
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length; // 일반적으로 16
// 해시버킷의 특정 인덱스에 데이터가 처음 저장되는 경우, 동작한다.
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// 해시버킷의 특정 인덱스가 null이 아닌 경우, 동작한다.
else {
Node<K,V> e; // 기존 Node
K k; // 기존 key
// 💡 기존 Node의 hash와 새로운 Node의 hash가 무조건 같아야함
// 기존 Node의 key값과 새로운 key의 참조가 같거나
// equals 비교 시, 두 Node가 논리적으로 같은 객체라면
// 두 Node는 동일한 식별자라고 판단한다.
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// 기존 Node가 TreeNode 인스턴스인지 확인한다.
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// 해당 해시버킷의 Node들을 순회한다.
for (int binCount = 0; ; ++binCount) {
// 해당 Node(p)의 다음 Node 참조가 null이라는 것은 마지막 Node까지 순회를 끝내다는 것이고
// 해당 해시버킷의 모든 노드들을 순회한 결과, 같은 식별자가 없다는 뜻이다.
// 맨 끝에 새로운 Node를 추가해주고 연결한다.
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// 해시버킷의 노드 수가 특정 임계값을 초과하면 트리로 전환한다.
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// 기존 Node와 새로운 Node가 같은 객체라면 순회를 멈추고 반복문을 벗어난다.
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 식별자에 해당하는 값을 새로운 값으로 변경한다.
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
Tree

- 트리는 계층구조를 표현하기에 제격이다.
- OS file system
- 데이터를 표현하는 덩어리를 노드라고 한다.
- 노드는 데이터를 담는 가장 작은 단위이다.
- 각 노드를 연결하는 라인을 edge라고 한다.
- 트리에서 최상위에 있는 노드는 root 노드라고 한다.
- 자식 노드가 없는 노드를 terminal 노드라고 한다.
- terminal 노드를 제외한 노드를 internal 노드라고 한다.
- 한 덩어리의 트리는 여러 개의 트리 집합으로 볼 수도 있다. (그림에 있는 서브트리의 집합)
- 트리는 자식 노드로 내려갈수록 레벨이 증가한다.
- 트리에서 가장 높은 레벨을 높이라고도 말한다.
- 위 트리의 높이는 3
Binary Tree

- 각각의 노드가 최대 2개의 자식 노드를 가질 수 있는 트리
- 자식 노드를 2개 or 1개 or 0개 가지고 있는 트리만 이진트리라고 할 수 있다.
Complete Binary Tree

- 트리의 마지막 레벨이 왼쪽부터 채워져있으면 Complete Binary Tree
- 최대 레벨을 제외한 나머지 레벨의 노드들은 (왼쪽부터)모두 채워져 있어야 한다.
full binary tree
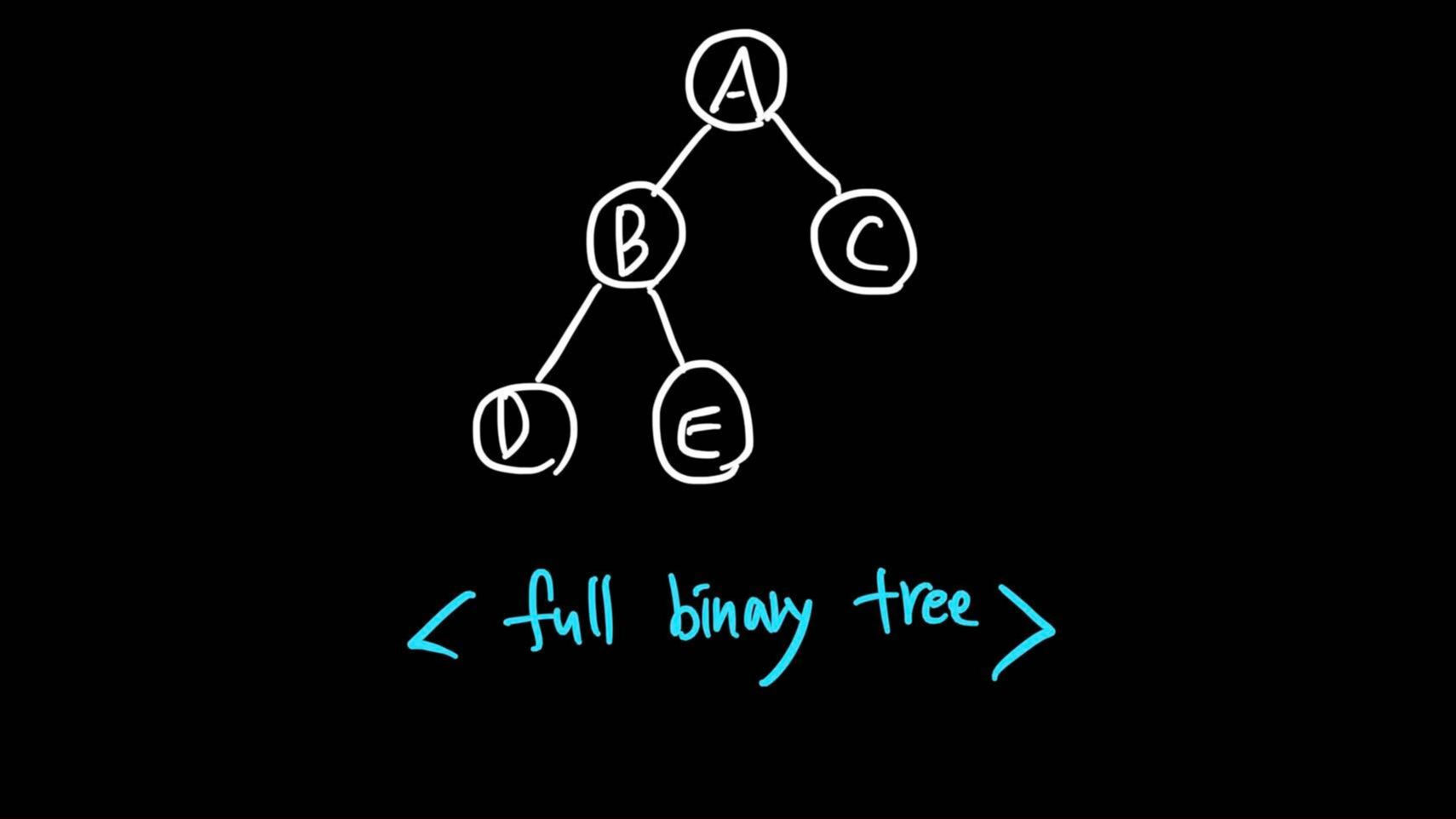
- 마지막 레벨의 노드를 2개 갖던가, 아예 없던가
Perfect Binary Tree
(한국에서 포화 이진 트리라고 부르고 Full Binary Tree라고 번역해놓은 경우가 있어서 좀 헷갈린다; 대체 무슨 이유일까?😂 암튼 걍 미국식으로 익히겠다.)

- 완벽하게 피라미드 구조를 이루고 있는 트리
- 레벨의 개수를 n이라고 가정할 때, Perfect Binary Tree 노드의 개수는 2^n - 1
이렇게 많은 종류의 트리를 배우는 이유는 또 다른 자료구조를 위한 것이다.
연결리스트를 배워서 앞으로만 넣고 앞으로만 빼는 규칙을 추가해 스택이라는 자료구조를 만들었고,
앞으로만 넣고 뒤로 빼는 규칙을 추가해 큐라는 자료구조를 만들었다.
트리도 마찬가지다.
단순한 트리구조에 여러 규칙을 추가해서 또 다른 자료구조를 만들 수 있으므로 여러 규칙이 있는 트리 구조를 배운 것이다.
📚 참고
Tree의 종류
https://woodcock.tistory.com/24
언급이 좀 되는 모 자료구조의 보조 해시 함수에 대한 이야기
그림으로 쉽게 배우는 자료구조와 알고리즘 (심화편)
'JAVA' 카테고리의 다른 글
| [F-Lab 모각코 챌린지 21일차] Binary Tree 순회 방법과 구현 (0) | 2023.06.28 |
|---|---|
| [F-Lab 모각코 챌린지 20일차] Lazy Loading / HashMap에 load factor가 존재하는 이유 / state machine (0) | 2023.06.27 |
| [F-Lab 모각코 챌린지 18일차] HashMap이 같은 Object를 판단하는 과정 / 주요 operation의 시간복잡도 (0) | 2023.06.25 |
| [F-Lab 모각코 챌린지 17일차] HashMap을 위한 HashTable (0) | 2023.06.24 |
| [F-Lab 모각코 챌린지 16일차] Set 인터페이스, HashSet 클래스 / LinkedList 클래스 (0) | 2023.06.23 |
댓글
이 글 공유하기
다른 글
-
[F-Lab 모각코 챌린지 21일차] Binary Tree 순회 방법과 구현
[F-Lab 모각코 챌린지 21일차] Binary Tree 순회 방법과 구현
2023.06.28 -
[F-Lab 모각코 챌린지 20일차] Lazy Loading / HashMap에 load factor가 존재하는 이유 / state machine
[F-Lab 모각코 챌린지 20일차] Lazy Loading / HashMap에 load factor가 존재하는 이유 / state machine
2023.06.27 -
[F-Lab 모각코 챌린지 18일차] HashMap이 같은 Object를 판단하는 과정 / 주요 operation의 시간복잡도
[F-Lab 모각코 챌린지 18일차] HashMap이 같은 Object를 판단하는 과정 / 주요 operation의 시간복잡도
2023.06.25 -
[F-Lab 모각코 챌린지 17일차] HashMap을 위한 HashTable
[F-Lab 모각코 챌린지 17일차] HashMap을 위한 HashTable
2023.06.24